这篇文章是==首篇将多目标强化学习算法应用到拥塞控制(CC)==的一篇偏应用的文章。现有的CC算法无法应对不同程序的新的需求,当应对新的应用时需要学习一个新模型,作者提出了MOCC多目标强化学习框架。在这个框架下,MOCC 进一步应用迁移学习将知识从过去的经验转移到新的应用程序中,即使是不可预见的,也能快速适应新的目标。
MOCC 明确地将性能目标纳入状态输入和动态奖励函数,并利用带有偏好子网络的新策略神经网络将不同目标与最优控制策略相关联。这允许 MOCC 有效地建立一个单一的相关模型来支持不同的性能目标。在此框架下,MOCC 进一步应用迁移学习,将过去经验中学到的知识快速迁移到新的应用程序中,并针对给定的目标优化 CC 算法。
总结一下:就是先预训练一个全局的普适模型,再根据每个应用的需求在应用上迅速地迭代,得到一个应用专属的CC。
这篇文章的多目标体现在,吞吐量,延迟等目标,不同应用对于这些目标的需求不同。本质上是多目标问题,与应用无关。感觉有点套了多目标的一个壳子,实际上就是一个简单的标量多目标问题,然后想办法让它适应不同的目标权重组合。
MOCC
MOCC结合了离线训练和在线学习。离线训练:MOCC在一组分布良好的目标上学习,将性能目标纳入状态输入和动态奖励函数,了解应用程序需求和最优策略之间的相关性。在线学习:面对新应用应用迁移学习经过几次迭代快速收敛到最优策略。
模型架构
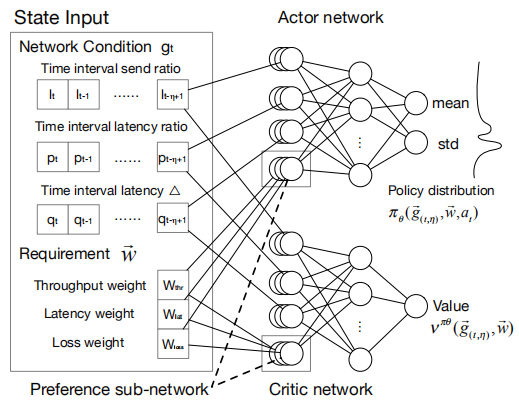
MOCC 对标准的基于 RL 的 CC 进行了两个主要更改:(1)将偏好子网络合并到策略网络中;(2)在状态输入和动态奖励功能中包括应用需求。这样,MOCC就可以建立各种应用需求和相应的最优码率控制策略之间的关联。
模型输入
模型的输入包含了网络的状态以及应用对于不同指标的需求。
- 应用对于不同指标的需求
这个需求用一个权重向量表示\(\vec{w}=<w_{thr},w_{lat},w_{loss}>\),$w_i( 0,1 ) \(,\)=1$。分别代表吞吐量、延迟和丢包率的权重。
- 网络的状态
模型的状态\(\vec{g}=<l_t,p_t,q_t>\)
\(l_t\):发送率。定义为发送方发送的数据包超过接收方确认的数据包
\(p_t\):潜伏期比率。当前时间间隔𝑡的平均潜伏期与历史上观察到的最小平均潜伏期之比
\(q_t\):延迟梯度。延迟时间对时间的导数
为了了捕捉网络动态的趋势和变化,模型使用==固定长度的网络统计历史==而不是最近的历史作为网络的输入:
\[ \vec{g}_{(t,\eta)}=<\vec{g}_{t-\eta},\vec{g}_{t-\eta+1},\cdots,\vec{g}_{t}> \]
输出
actor输出的是一个概率分布,agent挑选一个\(a_t\),网络发送速率\(x_t\)的变化如下: \[ x_t=\left\{ \begin{array}{l} x_{t-1}\times \left( 1+\alpha a_t \right) \ a_t>0\\ x_{t-1}/\left( 1-\alpha a_t \right) \ \ a_t<0\\ \end{array} \right. \] 这里 𝛼 是用于抑制振荡的比例因子。代替离散发送速率调整,我们选择连续发送速率调整以提高模型鲁棒性并实现更快的收敛。
奖励函数
\[ r_t=w_{thr}*O_{thr}+w_{lat}*O_{lat}+w_{loss}*O_{loss} \]
\(O_{thr}=\frac{\text{Measured\,\,Throughput}}{\text{Linked\,\,Capacity}}\),\(O_{lat}=\frac{\text{Base Link Latency}}{\text{Measured Latency}}\),\(O_{loss}=1-\frac{\text{Lost Packets}}{\text{Total Packets}}\),都定义为与奖励正相关,并且除以一个大数是为了标准化到\([0,1]\)。
模型结构
采用actor-critic的结构,两个模型都引入了==偏好子网络==。
训练
离线训练
显然,目标空间是无限的,为了高效训练MOCC,文章没有探索整个目标空间,而是在标志性目标的子集上进行训练。
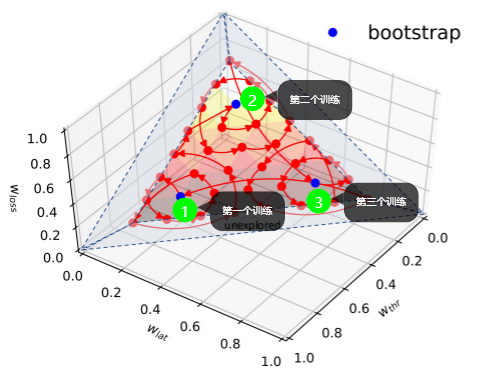
这一过程分为两个阶段:bootstrapping(引导)and fast traversing (快速遍历)
bootstrapping
选择一些bootstrapping的权重向量,也就是自定义一些权重向量。这些权重向量应当尽量有代表性,文章中是选取了3个不同的权重向量(目标),先在这三个上训练出了一个基础的模型。作者说这一过程需要花费数个小时。
文章中使用的3个bootstrapping目标为:\(<0.6,0.3,0.1>,<0.1,0.6,0.3>,<0.3,0.6,0.1>\)
==值得注意的是:这篇文章中的objectives的定义似乎和我理解的不一样,我理解的是吞吐量、延迟和丢包率是三个目标,而这篇文章中似乎把一个不同的权重向量\(\vec{w}=<w_{thr},w_{lat},w_{loss}>\)称为一个目标。详见文章的4.2小节。==
fast traversing
在快速遍历阶段,在基础模型的基础上,我们通过采用基于邻域的迁移学习策略来加速剩余的 𝜔-3 目标的训练 。该方法基于以下观察:==当两个 RL 具有相近的目标(即相似的权重向量)时,它们的最优解相近。==因此,在训练 RL 时,我们可以通过利用其相邻 RL 的解决方案来加速。
文章从一个目标迭代训练到它的neighbor,并以循环方式遍历所有目标。请注意,每次不会将一个权重向量训练到收敛,而只训练几个步骤以实现所有目标的平衡改进。当模型收敛到所有目标时,整个训练就完成了。如图所示:
neighbor的定义
两个权重向量定义为邻居,如果它们最多在两个维度上不同并且每个维度的差异小于步长。例如,在步长为 0.1 时,<0.2, 0.4, 0.4> 和 <0.2, 0.5, 0.3> 是邻居,<0.2, 0.4, 0.4> 和 <0.1, 0.5, 0.4> 是邻居,但 <0.2, 0.4, 0.4> 和 <0.1, 0.3, 0.6> 不是邻居。我们在邻居之间添加边并将所有边权重设置为 1
查找neighbor
查找neighbor使用的是dijkstra算法
𝐿 包含一个排序的目标列表,可以用作MOCC 模型的训练顺序

策略优化算法
使用PPO-Clip来训练MOCC \[ L^{CLIP}\left( \theta ,\vec{w} \right) _t=\hat{\mathbb{E}}_t\left[ \min \left( r_t\left( \theta \right) \hat{A}_t,clip\left( r_t\left( \theta \right) ,1-\epsilon ,1+\epsilon \right) \right) \hat{A}_t \right] \]
\(r_t(\theta)=\frac{\pi_\theta\left(a_t \mid \vec{v}_{(t, \eta)}, \vec{w}\right)}{\pi_{\theta_{o l d}}\left(a_t \mid \vec{v}_{(t, \eta)}, \vec{w}\right)}\),\(\hat{A}\left(\vec{g}_{(t, \eta)}, \vec{w}, a_t\right)=\sum_t \gamma^t r_t-V^{\pi_\theta}\left(\vec{g}_{(t, \eta)}, \vec{w}\right)\)其中\(V^{\pi _{\theta}}\left( \vec{g}_{\left( t,\eta \right)},\vec{w} \right)\)是一个惩罚项,为了使奖励不能始终为正,它是有critic网络估计的。
为了鼓励对策略网络的探索,正如过去的工作 [38] 中所建议的,我们在目标函数\(L^{CLIP}\)中添加了一个熵正则化项: \[ L_t^{C L I P+E}(\theta, \vec{w})=L^{C L I P}(\theta, \vec{w})+\beta H\left(\pi_\theta(\cdot \mid \vec{g}(t, \eta), \vec{w})\right) \]
在线调整
对于一个新应用,基础模型可以给出一个不错的CC方案,同时也可以通过迁移学习迭代少量次数做到很快适应应用,4.8分钟。
有一个问题:我们不想在适应新应用的同时牺牲旧应用的性能。与所有目标都是人工生成且均匀分布的离线训练不同,真实环境中的目标分布可能存在偏差:有些应用非常频繁,有些则很少见。在这种偏差下,传统的 RL 算法会过度拟合那些新的频繁应用,而逐渐忘记那些旧的稀有应用,这是不可取的。
为了避免这个问题,MOCC 使用了需求重放学习算法 。在线学习过程中,MOCC 存储长期遇到的应用(权重向量)。对于每个在线训练步骤,模型都在当前目标和从存储的应用程序池中随机抽取的旧目标上进行训练。将在线学习目标定义为: \[ L_{\text {online }}(\theta)=\frac{1}{2} *\left[L^{C L I P+E}\left(\theta, \vec{w}_i\right)+L^{C L I P+E}\left(\theta, \vec{w}_j\right)\right] \]



