本文提出了一种同时在多个任务上训练的强化学习方法，叫做Distral。主要的想法是把各个任务上学到的策略进行提纯（distill，本意是蒸馏）得到一个共有的策略，然后再使用这个共有的策略去指导各个特定任务上的策略进行更好的学习。文章称，这种多任务的强化学习方法避免了不同任务产生互斥的梯度，反而干扰学习；同时，也避免了各个任务学习进度不一致，导致某个任务的学习主导了整体的学习。
这个视频讲得不错，但是有一些错误，以自己笔记为准： https://www.bilibili.com/video/BV1PQ4y1M7nG?share_source=copy_web&vd_source=f038e298fba3a40848f18a2c0868db34
可以结合这篇文章来看：https://zhuanlan.zhihu.com/p/51091244
关于蒸馏学习，简单来说就是把一个模型的内容提炼到一个新的模型。可以看这篇：https://zhuanlan.zhihu.com/p/258390817
Distral
模型架构
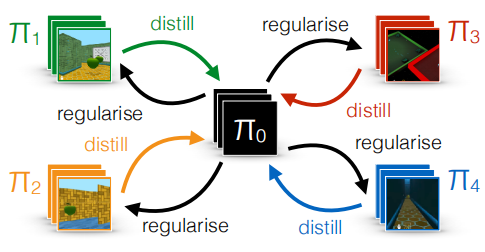
\(\pi_0\)是一个公共策略，是从\(\pi_1,\pi_2,\pi_3,\pi_4\)中蒸馏出来的一个中心策略。得到\(\pi_0\)后会用来指导\(\pi_1,\pi_2,\pi_3,\pi_4\)这四个不同的任务的策略。作者说这种基于蒸馏和迁移学习的多任务学习方式效果优于共享模型权重的方式。
目标函数
\[ \begin{aligned} J\left(\pi_0,\left\{\pi_i\right\}_{i=1}^n\right) &=\sum_i \mathbb{E}_{\pi_i}\left[\sum_{t \geq 0} \gamma^t R_i\left(a_t, s_t\right)-c_{\mathrm{KL}} \gamma^t \log \frac{\pi_i\left(a_t \mid s_t\right)}{\pi_0\left(a_t \mid s_t\right)}-c_{\mathrm{Ent}} \gamma^t \log \pi_i\left(a_t \mid s_t\right)\right] \\ &=\sum_i \mathbb{E}_{\pi_i}\left[\sum_{t \geq 0} \gamma^t R_i\left(a_t, s_t\right)+\frac{\gamma^t \alpha}{\beta} \log \pi_0\left(a_t \mid s_t\right)-\frac{\gamma^t}{\beta} \log \pi_i\left(a_t \mid s_t\right)\right] \end{aligned} \]
作者构造了上面这个目标函数，那么我们希望最大化这个目标函数。其中\(\alpha =\frac{c_{\text{KL}}}{c_{\text{KL}}+c_{\text{Ent}}}\)，\(\beta=\frac{1}{c_\text{KL}+c_\text{Ent}}\)，\(c_\text{KL}\)和\(c_\text{Ent}\)是决定KL和熵正则化强度的大小的标量因子，二者都是大于0的。
解释一下额外添加的两项的作用：
KL散度项正则化项：\(c_{\mathrm{KL}} \gamma^t \log \frac{\pi_i\left(a_t \mid s_t\right)}{\pi_0\left(a_t \mid s_t\right)}\)。约束了各个策略\(\pi_i\)不要离中心策略\(\pi_0\)太远。KL散度衡量了两个分布之间的差异，两个分布完全一致，散度就为0。否则散度较大。这里减去散度项，在使\(J\)尽可能大时，散度项就要尽可能小。
熵正则化项：\(-c_{\mathrm{Ent}} \gamma^t \log \pi_i\left(a_t \mid s_t\right)\)。鼓励探索，避免策略只会收敛到解决那个简单的任务。作者举了一个例子：在多任务场景下，如果有一个任务特别的简单，获得奖励非常容易。那么在没有熵正则化项的情况下，模型会收敛到解决那个简单任务然后不再去探索其他较难的任务。这会导致次优策略。这里这个熵项省略了一个乘数，不过并不影响理解它。因为熵的展开本身就存在一个负号，这里其实可以把负号看成一个整体，相当于加上了一个熵项。熵项越大说明策略不确定越高，越鼓励探索，与最大\(J\)的目标一致。
（正则化项：约束优化朝我们想要的方向前进）
两种优化方式
交替优化
交替优化就是指先蒸馏一个中心策略，再用中心策略去指导其他的任务。这样依次交替强化两种策略。
固定\({\pi_i}\)优化\(\pi_0\)
这实际上就是一个蒸馏过程，此时\(\pi_i\)项为常数，只需要最大化箭头右边的那项即可。可以用策略梯度等方法。
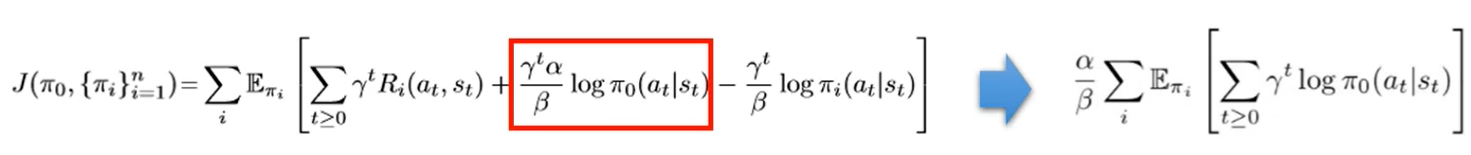
固定\({\pi_0}\)优化\(\pi_i\)
这样可以对每个\(\pi_i\)单独优化，可其看成一个附加熵项的单任务强化学习。推导过程如下：
这样奖励函数可以用soft Q Learning优化（详见自己的笔记）。
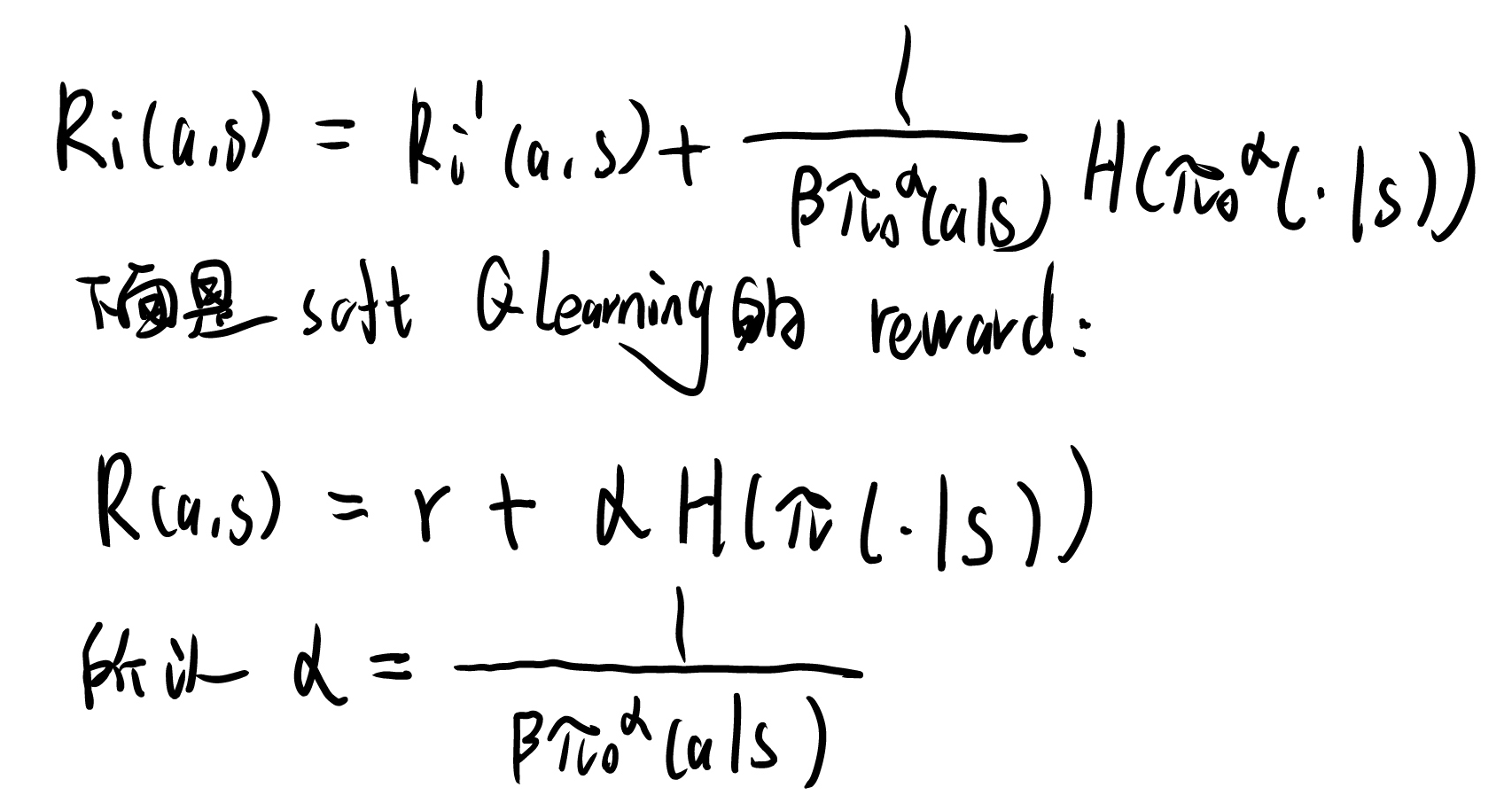
所以可以套用SQL的Q和V。带进去推一遍即可，得到Q和V。 \[ \begin{aligned} V_i\left(s_t\right) &=\frac{1}{\beta} \log \sum_{a_t} \pi_0^\alpha\left(a_t \mid s_t\right) \exp \left[\beta Q_i\left(a_t, s_t\right)\right] \\ Q_i\left(a_t, s_t\right) &=R_i\left(a_t, s_t\right)+\gamma \sum p_i\left(s_{t+1} \mid s_t, a_t\right) V_i\left(s_{t+1}\right) \end{aligned} \] 可以推出\(\pi_i\)
联合优化
依次对\(\pi_i\)和\(\pi_0\)做SGD，最大化目标函数。联合优化比较简单
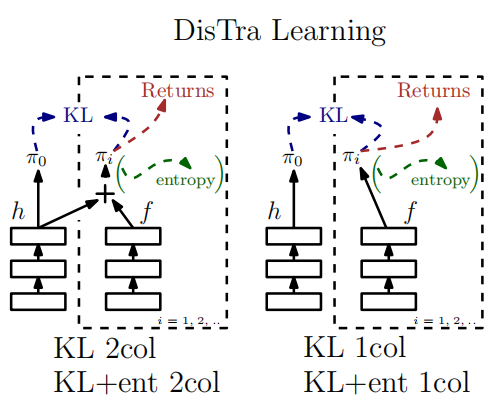
更好的策略表示
\(\pi_0\)的估计可以使用简单的玻尔兹曼策略表示，这里的\(h_\theta(a_t|s_t)\)就是代表\(Q_\theta\) \[ \hat{\pi}_0\left(a_t \mid s_t\right)=\frac{\exp \left(h_{\theta_0}\left(a_t \mid s_t\right)\right.}{\sum_{a^{\prime}} \exp \left(h_{\theta_0}\left(a^{\prime} \mid s_t\right)\right)} \] 对于\(\pi_i\)，作者提出了一个更好的表示方式。用\(\pi_0\)的共有部分和自己的特有部分来表示。
\[
\hat{\pi}_i\left(a_t \mid s_t\right)=\hat{\pi}_0^\alpha\left(a_t \mid s_t\right) \exp \left(\beta \hat{A}_i\left(a_t \mid s_t\right)\right)=\frac{\exp \left(\alpha h_{\theta_0}\left(a_t \mid s_t\right)+\beta f_{\theta_i}\left(a_t \mid s_t\right)\right)}{\sum_{a^{\prime}} \exp \left(\left(\alpha h_{\theta_0}\left(a^{\prime} \mid s_t\right)+\beta f_{\theta_i}\left(a^{\prime} \mid s_t\right)\right)\right.}
\]
策略梯度
于是就利用策略梯度对\(\pi_i\)和\(\pi_0\)分别优化。 \[ \begin{aligned} \nabla_{\theta_i} J &=\mathbb{E}_{\hat{\pi}_i}\left[\left(\sum_{t \geq 1} \nabla_{\theta_i} \log \hat{\pi}_i\left(a_t \mid s_t\right)\right)\left(\sum_{u \geq 1} \gamma^u\left(R_i^{\mathrm{reg}}\left(a_u, s_u\right)\right)\right)\right] \\ &=\mathbb{E}_{\hat{\pi}_i}\left[\sum_{t \geq 1} \nabla_{\theta_i} \log \hat{\pi}_i\left(a_t \mid s_t\right)\left(\sum_{u \geq t} \gamma^u\left(R_i^{\mathrm{reg}}\left(a_u, s_u\right)\right)\right)\right] \end{aligned} \] 其中：\(R_i^{\operatorname{reg}}(a, s)=R_i(a, s)+\frac{\alpha}{\beta} \log \hat{\pi}_0(a \mid s)-\frac{1}{\beta} \log \hat{\pi}_i(a \mid s)\) \[ \begin{aligned} \nabla_{\theta_0} J=& \sum_i \mathbb{E}_{\hat{\pi}_i}\left[\sum_{t \geq 1} \nabla_{\theta_0} \log \hat{\pi}_i\left(a_t \mid s_t\right)\left(\sum_{u \geq t} \gamma^u\left(R_i^{\mathrm{reg}}\left(a_u, s_u\right)\right)\right]\right.\\ &+\frac{\alpha}{\beta} \sum_i \mathbb{E}_{\hat{\pi}_i}\left[\sum_{t \geq 1} \gamma^t \sum_{a_t^{\prime}}\left(\hat{\pi}_i\left(a_t^{\prime} \mid s_t\right)-\hat{\pi}_0\left(a_t^{\prime} \mid s_t\right)\right) \nabla_{\theta_0} h_{\theta_0}\left(a_t^{\prime} \mid s_t\right)\right] \end{aligned} \]
