本文研究了权重变化的多目标强化学习方式。
==主要贡献:==
- 提出了一种能够适应动态权重变化的多目标Q-Learning方式(CN)。
- 提出了多样化经验化回放缓存(DER)保存多样化的经验,使模型能够从过去的不同的权重的经验中获取对当前权重设置有益的经验,实验证明DER对于动态权重变化的强化学习方式提升很大。
- 为多目标强化学习提出了一个新的benchmark-矿车(Minecart)。
这篇文章的多目标采用线性标量函数的方式实现。
Conditioned Network(CN)
CN的模型结构
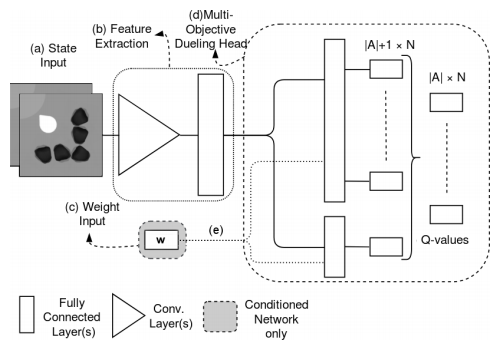
采用的Dueling Q Network(具体见蘑菇书),输入有两个值:
state:由于CN是端到端的,输入的是一张图像,经过特征提取后变成一个state向量输入。
weight:各个目标的权重向量
训练过程
我们希望CN能够适应动态的权重变化,所以在一味地在当前的权重向量(active weight vector)上训练是不行的。我们希望CN在拟合当前weight的基础上不遗忘过去的weight。所以样本一次应该在多个权重向量上进行训练。
文章中的做法就是在当前的权重向量\(w_t\)和一个随机的先前遇到的权重向量\(w_j\)上平均地求损失。\(Q_{CN}^{-}\)是target net,CN采用Double Q-Learning的方式。 \[ \begin{aligned} &\frac{1}{2}\left[\left|\mathbf{y}_{\mathbf{w}_t}^{(j)}-\mathbf{Q}_{C N}\left(a_j, s_j ; \mathbf{w}_t\right)\right|+\left|\mathbf{y}_{\mathbf{w}_j}^{(j)}-\mathbf{Q}_{C N}\left(a_j, s_j ; \mathbf{w}_j\right)\right|\right] \\ &\mathbf{y}_{\mathbf{w}}^{(j)}=\mathbf{r}_j+\gamma \mathbf{Q}_{C N}^{-}\left(\underset{a \in A}{\operatorname{argmax}} \mathbf{Q}_{C N}\left(a, s_{j+1} ; \mathbf{w}\right) \cdot \mathbf{w}, s_{j+1} ; \mathbf{w}\right) \end{aligned} \]
算法步骤

整体就是一个典型的Q-Learning过程,这里要维护两个Buffer,\(W\)存储过去的权重向量 ,\(D\)存储经验。
\(getWeightVector()\)这个函数用来获取active weight即\(w_t\),在后续实验中提到了两种不一样的生成方式。
Diverse Experience Replay(DER)
动机
以前的Q-Learning包括上面的CN都是选择维护了一个先进先出的缓存,粗暴地存储了最近的以往的经验。但是文章中说了,一个以往的weight的经验可能对于当前的weight的训练是有害的。==我们希望在缓存中保存那些对于当前weight训练有益的经验(有益的经验就是指与当前weight尽可能相关的经验)。==因为weight变化是随机的,那么在我们不知道未来会采用什么样的weight前提下,==我们希望使缓冲区中经验尽可能的多样化(diverse)。==这样在当前weight(active weight)训练时随机选就有可能选到对自己训练有益的经验。
比较容易想到的就是增大缓冲区,但是这是不可行的。文章列出了两点理由:
- 除非回放缓冲区是无限的,否则在到达需要它们的权重空间区域之前,仍然需要擦除旧的经验。
- 即使这些相关经验仍然存在,由于总数过多,我们比较难以选到这些经验。
所以文章提出了DER。
DER
DER将trajectory(一段完整的状态-动作序列)作为原子单位处理,这样做是为了便于获取从终止状态到初始状态间的完整的Q值。
使用签名函数\(s\)为每个trajectory计算一个签名(signature),当考虑将trajectory添加入Buffer时,多样性函数\(d\)根据签名计算每个trajectory的与buffer中其他trajectory的相对多样性。如果新trajectory的加入增加了缓冲区的整体多样性,则仅将新trajectory添加到多样化缓冲区中。当它已满时,对多样性贡献最小的trajectory将从多样性缓冲区中弹出。
在动态权重中使用DER
- 每个回合的转换被视作一条trajectory
- 签名函数\(s\left( \tau \right) =\sum_{t=0}^{\left| \tau \right|}{\gamma ^tr_t}\)
- 使用crowding distance算法作为多样性度量(算法没去看)
在动态权重中,也保留了一个FIFO的buffer,只有当FIFO buffer满了时才会将最老的trajectory尝试加入DER。
在训练时会现在DER中采样训练,然后在FIFO buffer中进一步训练。
新的Benchmark-Minecart
简略写一下,详见论文。
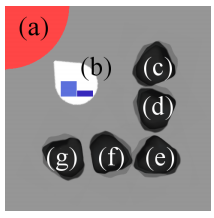
b代表矿车,c~g代表不同的矿坑,每回合里面会随机生成不同的矿石。a代表矿石出售点。
reward vector包含\(N\)维前\(N-1\)维代表矿石的数量,第\(N\)维代表燃料消耗。
以往的算法用在动态权重下
为了实验中方便比较以往的多目标算法,文章还调整传统的MORL以适应动态权重。
UVFA
没看过这个算法,先pass
Multi-Network(MN)
实际上这种方式非常的暴力,就是将传统的标量化DQN在多个不同的weight上训练,将不同weight下的最优策略存储进一个Buffer中\(\Pi\)。这里的\(\Pi\)不会太大,因为它是CSS的子集(CSS就是在任意weight下最优策略的集合)。而CSS不会太大。这一点在Minecraft中有说明过,下图的一个区域代表这一区域中最优策略是一致的。实际上也就是只有7块。
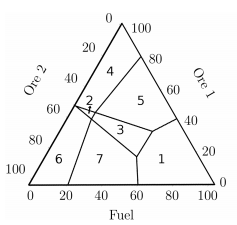
替换规则:
对于当前的\(w\)训练得到一个最优的\(\pi_w\),如果\(V^{\pi_w}\)对于至少一个过去的权重向量或当前的权重向量 w 改进了\(\Pi\)中的策略的最大标量值,则将其保存。数学语言表示更加清晰: \[ \exists w\in W,\ V^{\pi _t}\cdot w>\max _{V'\in \Pi}V'\cdot w-\kappa \] 其中,\(\kappa\)是一个常数,是为了解决近似误差问题。当两个标量化值在彼此的误差 κ 内时,较新的策略更受青睐。
此时,将\(\pi_w\)加入\(\Pi\)。所有被 \(\pi_w\) 冗余的旧策略都从\(\Pi\)中删除。如果\(\pi_w\)对于任何遇到的权重向量都不是最佳策略,那么它自己就是冗余的。
训练新的weight:
当训练一个新\(w\)时,会从\(\Pi\)中选一个\(\pi'\)使得\(V^{\pi'}\cdot\pi'\)最大。在\(\pi'\)的基础上训练,这样训练起来比较快。
MN有一个很大的缺点,因为MN 基于预测的 Q 值比较策略,所以不准确的输出会通过使 MN 偏向于高估的策略来干扰训练。因此,MN 需要对每个权重向量进行长时间的训练才能获得准确的值进行比较。==可想而知MN是比较慢的。==
实验
评判指标:
最优策略的价值与实际reward之间的差值:\(\varDelta= V_{w}^*\cdot w-\sum_{t=0}^T{\gamma^{t}r_t\cdot w}\),\(V_w^*\)代表\(w\)下的最优策略的value。\(\varDelta\)显然是越小越好。
文章讨论了两种不同的\(w\)的生成方式:
- 稀疏情况:从Dirichlet分布 (\(\alpha=1\)) 中随机采样的,对于Minecart,每 50k步采样一次,对于 DST,每 5k步采样一次。
- 固定的变化:\(w\)在10个回合内线性地变化到\(w'\)
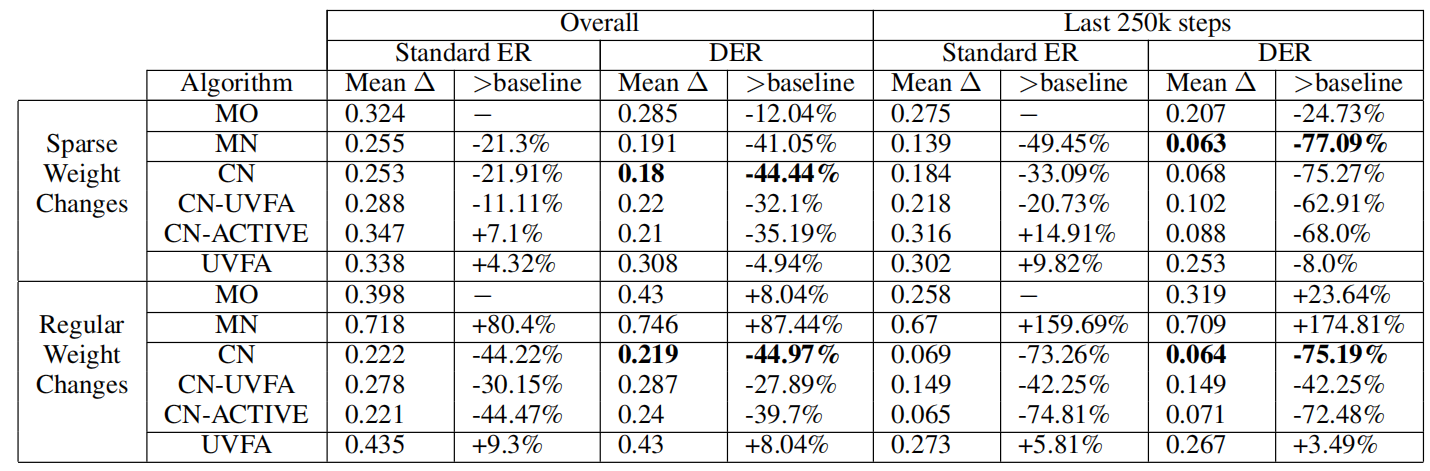
MO:单个多目标 DQN 通过标量化Q-Learning仅在当前 w 上持续训练(不维护多个网络)。
CN:CN与UVFA相结合
CN-ACTIVE:CN仅在当前的w上训练。



